접미사 배열
접미사 배열이란, 어떤 문자열의 접미사를 사전식 순서대로 나열한 배열을 의미합니다. 즉 아래 예시처럼 문자열 "banana"의 모든 접미사들을 정렬한 배열이라고 할 수 있습니다.
<banana의 접미사>
0 banana 5 a
1 anana Sort the Suffixes 3 ana
2 nana ----------------> 1 anana
3 ana alphabetically 0 banana
4 na 4 na
5 a 2 nana
접미사 배열 구하기
접미사 배열을 구현하는 알고리즘에는, Naive 알고리즘과 Manber-Myers 알고리즘이 있습니다.
Naive 알고리즘
접미사 배열을 만드는 가장 쉬운 방법으로, 단순히 비교 정렬 알고리즘을 이용해서 구현하는 방식입니다.
문자열의 길이가 n이라고 할 때, 접미사는 n개가 만들어집니다. 그리고 이 n개의 접미사들을 정렬할 때 필요한 비교 횟수는 O(n*logn)으로 나타낼 수 있습니다. 그리고, 각 비교 횟수마다 두 접미사를 사전순으로 정렬하는 방법은 모든 문자에 대해 대소비교를 하는 것이기 때문에 접미사 최대 길이인 O(n) 번의 비교가 발생하게 됩니다.
따라서, 이렇게 Naive 하게 구성하는 경우에는 시간 복잡도가 아래와 같습니다.

이 시간 복잡도는 n이 커질수록 상당히 시간이 걸리기 때문에, 이보다 더 줄인 방법인 Manber-Myers 알고리즘을 사용해야 합니다.
Manber-Myers 알고리즘
- 접미사 배열을 생성하기 위해 정렬 시 매 비교마다 각 접미사의 t번째 글자를 기준으로 정렬을 합니다. 이 때 t는 2배씩 증가합니다.
- 이렇게 정렬할 수 있는 이유는, 이전에 비교한 결과를 이용하여 두 문자열의 대소 비교를 하기 때문입니다. 그래서 두 문자열의 대소비교를 O(1) 만에 끝낼 수 있습니다.
- Manber-Myers 알고리즘에 필요한 배열은 크게 3가지가 있습니다.
- suffixArr [i]: 문자열을 이루는 각 문자의 인덱스라고 생각하면 됩니다. (banana의 경우, suffixArr [i] = {0,1,2,3,4,5})
- group [i]: suffixArr [i]부터 시작하는 접미사가 속한 그룹 번호입니다. 첫 글자가 같으면 같은 그룹 번호를 가지는 것으로 시작합니다. (banana의 경우, group [i] = {1,0,13,0,13,0}, 여기서 그룹 번호는 (문자-'a')로 할당했습니다.)
- 매 t번째 글자를 기준으로 정렬한 뒤, t번째 글자가 같은 것끼리 같은 그룹으로 묶습니다. 이 과정을 t=1~n 동안 반복합니다.
- 비교되는 두 문자열 중 하나가 t보다 짧은 경우를 대비해 group [n]=-1로 초기화합니다. (n은 문자열 길이)
- new_group [i]: group [i]를 갱신하기 전에 그룹 정보를 저장하는 임시 배열입니다.
- 이렇게 접미사 배열을 생성하면 아래의 시간복잡도를 가집니다. (quick sort 사용)

- counting sort(계수 정렬)을 이용하면 더 빠른 시간 (n*logn) 안에 suffix array를 생성할 수 있습니다.
그림으로 확인해 보겠습니다.
맨 처음 banana의 suffix array입니다.

우선, 첫 한 글자를 기준 (t=1)으로 각 접미사 배열을 정렬하면 아래와 같이 결과가 나옵니다.

그 후, 각 접미사의 두 번째 글자 (t=2) 기준으로 정렬하면 아래와 같은 결과가 나옵니다.

마지막으로, 각 접미사의 네 번째 글자(t=4) 기준으로 정렬하면 아래와 같은 결과가 나옵니다. (t <n까지(n은 6) 정렬하므로 t=4가 마지막 단계입니다.)

위 과정을 코드로 구현하면 아래와 같습니다.
코드 구현 (quick sort)
#include<stdio.h>
#define Max 1001
char string[Max];
int N;
int suffixArr[Max],
group[Max],
newgroup[Max];
int cmp(int small, int big, int t) {
if (group[small] != group[big])
return group[small] < group[big]; // 그룹이 다르면 그룹번호가 작은 것이 앞으로
else // 그룹이 같으면 t번째 문자로 정렬
return group[small + t] < group[big + t];
// 정확히 말하면, t번째 문자로 시작하는 접미사 배열의 그룹 번호로 정렬
}
void quick(int above, int below, int t) {
if (above >= below)
return;
int left = above - 1,
right = below + 1,
pivot = suffixArr[left + (right - left) / 2];
while (left < right) {
while (cmp(suffixArr[++left], pivot, t));
while (cmp(pivot, suffixArr[--right], t));
if (left >= right)break;
int temp = suffixArr[left];
suffixArr[left] = suffixArr[right];
suffixArr[right] = temp;
}
quick(above, left - 1, t);
quick(right + 1, below, t);
}
void getSuffixArr() {
//1.초기화 , 그룹, suffixArr
for (N = 0; string[N]; N++)
suffixArr[N] = N,
group[N] = string[N] - 'a'; // 문자 1개로 grouping (t=0)
group[N] = -1; // 문자가 없는 부분 ('\0')
//2. 정렬
int t = 1;
while (t < N) {
quick(0, N - 1, t);
// 임시 배열에 그룹 갱신
// suffixArr의 0번째 접미사 배열의 그룹 넘버는 0으로 시작
newgroup[suffixArr[0]] = 0;
newgroup[N] = -1;
for (int i = 1; i < N; i++)
if (cmp(suffixArr[i - 1], suffixArr[i], t)) // 두 접미사 배열의 t 번째 문자 비교
newgroup[suffixArr[i]] = newgroup[suffixArr[i - 1]] + 1;
else // t번째 문자가 같다면 같은 그룹
newgroup[suffixArr[i]] = newgroup[suffixArr[i - 1]];
//3. 그룹최신화
for (int i = 0; i < N; i++)
group[i] = newgroup[i];
t <<= 1; // t *=2;
}
}
int main() {
scanf("%s", string);
getSuffixArr();
return 0;
}
int cmp(int small, int big, int t) {
if (group[small] != group[big])
return group[small] < group[big]; // 그룹이 다르면 그룹번호가 작은 것이 앞으로
else // 그룹이 같으면 t번째 문자로 정렬
return group[small + t] < group[big + t];
// 정확히 말하면, t번째 문자로 시작하는 접미사 배열의 그룹 번호로 정렬
// 왜냐하면, group[small] == group[big]라는 말은, 두 접미사 배열이 t-1번째까지는
// 같은 문자로 이루어져 있다는 의미이므로
// t번째 문자부터 시작하는 접미사 배열 그룹 번호로 비교한다.
}
- 이 부분이 Suffix Array의 핵심 코드라고 생각합니다.
- 저는 이 알고리즘을 공부하면서 t를 2배씩 증가시키는데 어떻게 모든 문자들을 빠짐없이 정렬할 수 있을까 하는 궁금증이 있었습니다. 이것을 가능하게 하는 것이 바로 위 코드의 t번째 문자부터 시작하는 접미사 배열 그룹 번호로 비교하는 부분입니다. (group [small+t] < group [big+t])
- 예를 들어, abcd에서 abcd의 c는 a로 시작하는 접미사 배열에서 3번째 위치한 원소로 t가 2배씩 증가하므로 비교 연산에 포함되지 않을 것 같지만, 실제로 c는 c로 시작하는 접미사 배열(cd)의 1번째 원소입니다. 즉, c가 abcd와 다른 접미사 배열의 비교에 사용되지 않아도, cd를 이용하여 정렬할 때는 c가 비교에 사용됨으로써 모든 문자들이 결국에는 정렬 시 비교 연산에 사용되는 원리입니다.
- 결국엔, 이미 정렬 비교에 사용된 접미사 배열들을 가져다 씀으로써 중복되는 비교를 없애 시간 복잡도를 줄였다고 볼 수 있습니다.
아래는 Suffix Array를 정렬해 가는 과정을 단계별로 출력해 보았습니다.
예시 문자열

- 맨 처음 초기화
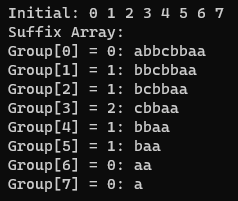
- t=1 (각 접미사 배열의 첫 번째 문자로 비교)
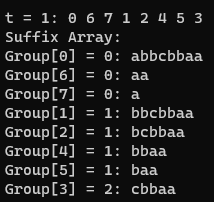
- t=2: (각 접미사 배열의 두 번째 문자로 비교)
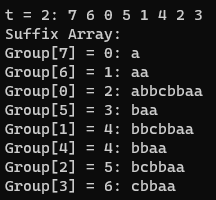
- t=4: (각 접미사 배열의 네 번째 문자로 비교)
보통 Suffix Array (접미사 배열)은 단독으로 사용되기보다는 LCP (Longest Common Prefix array, 최장 공통 접두사 배열)과 함께 사용되는 알고리즘입니다.
LCP
최장 공통 접두사 배열은 Suffix Array (접미사 배열)에서 이전 접미사와 공통되는 접두사의 길이를 저장한 배열입니다.
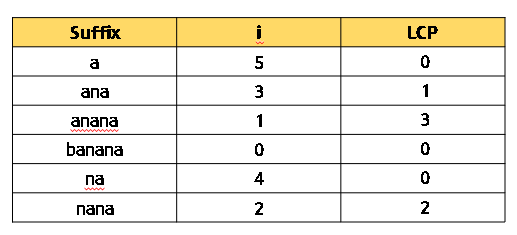
이 알고리즘 또한, Suffix Array 알고리즘과 비슷하게 인접한 접미사끼리 비교할 때 중복해서 비교하지 않도록 구현함으로써 O(n) 만에 공통 접두사 길이를 구할 수 있도록 하였습니다.
참고로 LCP는 알고리즘 대회에서 어떤 문자열(S [i])이 주어졌을 때, 2번 이상 반복되는 연속된 부분 문자열의 최대 길이를 구할 때 주로 사용된다고 합니다.
LCP가 어떻게 이 문제를 해결할 수 있는지 간략하게 설명해 보면, 문자열 S [i]의 어떤 부분 문자열은 결국에는 주어진 문자열(S [i])의 접미사의 접두사 (e.g. abcd의 부분 문자열 bc는 접미사 bcd의 접두사)라는 점을 이용하여 Suffix Array의 인접한 접미사끼리 공통되는 접두사 중 가장 긴 것을 찾아내도록 해 줍니다.
코드 구현
#include<stdio.h>
#define Max 1001
int N; // 문자열 길이
int lcp[Max];
int suffixArr[Max]; // Suffix Array 알고리즘으로 구한 접미사 배열
char str[Max];
int rank[Max];
void LCP() {
for (int i = 0; i < n; i++)
rank[suffixArr[i]] = i;
int h = 0;
for (int i = 0; i < N; i++) {
if (rank[i]) {
int prev = suffixArr[rank[i] - 1];
while (str[prev + h] == str[i + h]) h++;
lcp[rank[i]] = h;
}
h = max(h - 1, 0);
}
}
접미사 배열 관련 문제
[백준 문제]
1605 반복 부분문자열 - 소스코드
11479 서로 다른 부분 문자열의 개수2 - 소스코드
[참고자료]
접미사 배열(Suffix Array)
Suffix Array란, 문자열 S가 있을 때 그 접미사들을 정렬해 놓은 배열이다. 예를 들어, 문자열 S=banana의 접미사는 아래와 같이 총 6개가 있다.Suffixibanana1anana2nana3ana4na5a6이를 Suffix 순으로 정렬하면 아
www.crocus.co.kr
https://movefast.tistory.com/287
접미사 배열(Suffix Array)과 최장 공통 접두사 배열(LCP Array)
접미사 배열 접미사 배열이란 어떤 문자열의 접미사를 사전식 순서대로 나열한 배열을 말한다. by Wikipedia 문자열 "banana" 의 접미사는 다음과 같다. Suffix Array: 0: banana 1: anana 2: nana 3: ana 4: na 5: a 사
movefast.tistory.com
Suffix Array와 LCP
Suffix Array (접미사 배열) Suffix Array(韓: 접미사 배열)은 어떤 문자열의 suffix(접미사)들을 사전순으로 나열한 배열을 의미한다. 문자열 관련된 문제에서 자주 쓰이는 방법이다. 예를 들어, 문자열 $S
blog.myungwoo.kr
https://gist.github.com/koosaga/44532e5dec947132ee55da0458255e05
sfxarray.cpp
GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
'Algorithms' 카테고리의 다른 글
| 해시 함수 (Hash Table) (0) | 2023.12.13 |
|---|---|
| C언어 - Quick sort 구현 (0) | 2023.12.10 |
| C언어 - 문자열 탐색, 비교 구현해보기 (0) | 2023.12.09 |
| 비트 연산 활용 (4) | 2023.12.03 |
| 그리디 알고리즘 (Greedy)과 다이나믹 프로그래밍 (DP) (0) | 2023.10.18 |
