이번 포스팅에서는 실제로 데이터를 이용하여 데이터 전처리부터 특정 머신러닝 모델을 활용하여 학습을 하는 과정까지를 정리해 보았습니다.
1. 데이터 준비
아래와 같이 diabetes 데이터를 불러옵니다. 이 데이터를 통해 우리는 Outcome 변수를 예측해야 합니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv("diabetes.csv")
df.head()
2. EDA
a. 시각화 1
먼저 종속변수 Outcome의 평균이 컬럼별로 어떤지 시각화해 보겠습니다.
diabetes = df.groupby('Outcome').mean()
fig, axes = plt.subplots(2,4, figsize=(20,14))
for i in range(4):
sns.barplot(diabetes.index, diabetes.iloc[:, i], ax = axes[0][i])
axes[0][i].set_title(diabetes.columns[i])
for i in range(4):
sns.barplot(diabetes.index, diabetes.iloc[:, i+4], ax = axes[1][i])
axes[1][i].set_title(diabetes.columns[i + 4])
위 그림에서 볼 수 있듯이 모든 컬럼들이 Outcome이 1인 데이터의 평균이 0인 데이터보다 크다는 것을 알 수 있습니다.
b. 다중공선성 확인
다음으로는 독립변수끼리 강한 상관관계를 가지고 있는지 correlation 값과 vif 값을 이용하여 확인해 보겠습니다.
sns.heatmap(df.drop(columns='Outcome').corr(), annot=True)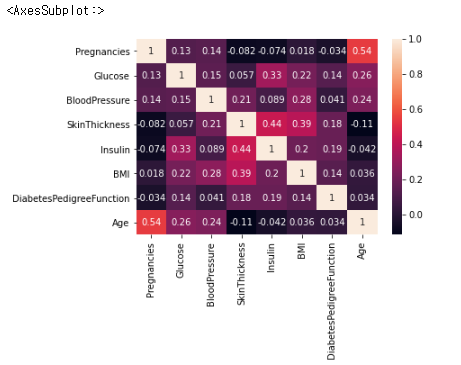
우선 Correlation Matrix에서 강한 상관관계가 있는 독립변수는 없는 것 같습니다. (보통 0.7 이상이면 상관관계가 꽤 있다고 봅니다.) 여기까지 해서 다중공선성 확인을 마무리할 수 있지만 VIF를 통해 한 번 더 확인해 보도록 하겠습니다.
from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF
from patsy import dmatrices
y, X = dmatrices('Outcome ~ '+'+'.join(df.drop(columns='Outcome').columns[:]), data=df)
vif_df = pd.DataFrame()
vif_df['VIF'] = [VIF(X, i) for i in range(len(df.drop(columns='Outcome').columns)+1)]
vif_df['Columns'] = ['Intercept']+ df.drop(columns='Outcome').columns.tolist()
vif_df = vif_df.set_index('Columns')
vif_df
위 그림에서도 독립변수의 VIF 값이 크지 않습니다 .(보통 10 이상이면 다중 공선성이 있다고 판단합니다.) 따라서, drop 해야 할 독립변수는 없어 보입니다.
c. 이상치 확인
이번에는 각 컬럼별로 이상치를 확인해 보겠습니다. 먼저 아래는 seaborn의 boxplot 함수를 이용하여 이상치 유무를 시각화한 결과입니다.
columns = df.drop(columns='Outcome').columns
fig, axes = plt.subplots(2, 4, figsize=(20, 14))
for i in range(4):
sns.boxplot(data=df[columns[i]], ax = axes[0][i])
axes[0][i].set_title(columns[i])
for i in range(4):
sns.boxplot(data=df[columns[i+4]], ax = axes[1][i])
axes[1][i].set_title(columns[i + 4])
Boxplot 결과, 여러 개의 컬럼에서 이상치가 존재하는 것 같습니다. 그중에서 Age 변수의 이상치를 제거하고, 0이 존재하면 안되는 Glucose 값과 BloodPressure 값을 전처리 해 보겠습니다.
q3 = df['Age'].quantile(0.75)
q1 = df['Age'].quantile(0.25)
iqr = q3-q1
m = df['Age'].mean()
outlier_index = df[(df['Age']>=m + iqr)].index
sub_df1 = df.copy()
sub_df1.loc[outlier_index, 'Age'] = df['Age'].median() # 이상치 제거
sns.boxplot(sub_df1['Age'])
outlier_index2 = df[df['Glucose']==0].index
sub_df1.loc[outlier_index2, 'Glucose'] = sub_df1['Glucose'].median()
outlier_index3 = df[df['BloodPressure']==0].index
sub_df1.loc[outlier_index3, 'BloodPressure'] = sub_df1['BloodPressure'].median()
d. OverSampling
종속변수 Outcome의 데이터의 분포를 보면 Outcome이 0인 데이터가 Outcome이 1인 데이터보다 더 많이 포함되어 있습니다. Outcome이 1인 데이터를 Oversampling 하여 Outcome 데이터를 균형 있게 만들어 보겠습니다. (RandomOverSampler 이용)
from imblearn.over_sampling import RandomOverSampler
X = sub_df1.drop(['Outcome'], axis=1)
y = sub_df1[['Outcome']]
ros = RandomOverSampler()
X_oversampling, y_oversampling = ros.fit_resample(X,y)
print('기존')
print(sub_df1['Outcome'].value_counts()/len(sub_df1))
print('-'*10)
print('Oversampling 후')
print(y_oversampling['Outcome'].value_counts()/len(y_oversampling))
3. Model 학습
EDA도 어느 정도 마쳤으니 이제 Model을 실제로 학습시켜 보겠습니다. 3가지 모델인 LogisticRegression, XGBClassifier, Support Vector Classifier을 활용하여 각 모델의 학습 속도와 학습 정확도를 비교해 보겠습니다.
from sklearn.linear_model import LogisticRegression
from xgboost import XGBClassifier
from sklearn.svm import SVC
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.metrics import accuracy_score
import time
from imblearn.over_sampling import SMOTE
# 모델 준비
log = LogisticRegression()
xgb = XGBClassifier()
svm_clf = SVC(kernel='linear')
# OverSampling - SMOTE를 이용
smote = SMOTE(random_state=0)
# KFold 교차검증
kfold = KFold()
def model_result(model):
pred_li=[]
for train_index, test_index in kfold.split(X):
X_train, X_test = X.iloc[train_index,:], X.iloc[test_index,:]
y_train, y_test = y.iloc[train_index, :], y.iloc[test_index,:]
X_train_resample, y_train_resample = smote.fit_resample(X_train, y_train) # Oversampling
start = time.time()
model.fit(X_train_resample, y_train_resample)
end=time.time()
pred = model.predict(X_test)
pred_li.append(accuracy_score(pred, y_test['Outcome']))
print(f"{end-start:.5f} sec")
print(np.mean(pred_li))
print(model_result(log)) # 시간: 0.03257 sec, 정확도: 0.756574144809439
print(model_result(xgb)) # 시간: 0.15453 sec, 정확도: 0.729191070367541
print(model_result(svm_clf)) # 시간: 2.48340 sec, 정확도: 0.7734997029114675
학습 결과, Support Vector 머신의 정확도가 가장 높았고, Logitic Regression 모델의 속도가 가장 빨랐습니다.
위에서 학습 속도를 조금 더 줄이기 위하여 PCA를 이용한 주성분 추출을 통해 학습 데이터의 차원을 줄여보겠습니다.
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
def pca_model_result(model):
pred_li = []
for train_index, test_index in kfold.split(X):
X_train, X_test = X.iloc[train_index,:], X.iloc[test_index, :]
y_train, y_test = y.iloc[train_index,:], y.iloc[test_index, :]
# OverSampling with SMOTE
X_train_resample, y_train_resample = smote.fit_resample(X_train, y_train)
# Scaling for PCA
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_resample)
X_test_scaled = scaler.transform(X_test)
# PCA
pca = PCA(n_components=5)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled) # fit_transform 아님!
start = time.time()
model.fit(X_train_pca, y_train_resample)
end = time.time()
pred = model.predict(X_test_pca)
pred_li += [accuracy_score(y_test, pred)]
print(f'time: {end-start} sec')
print(np.mean(pred_li))
print(pca_model_result(log)) # 시간: 0.004052162170410156 sec, 정확도: 0.7487649605296663
print(pca_model_result(xgb)) # 시간: 0.15052270889282227 sec, 정확도: 0.7005602240896358
print(pca_model_result(svc)) # 시간: 0.01500 sec, 정확도: 0.7422544775485951
PCA를 통해 데이터의 차원을 줄이니 학습 속도는 아까보다 빨라졌습니다. 하지만 정확도 측면에서 조금 떨어지네요. 만약 데이터의 개수가 더 많다면 PCA 사용 시, 학습 속도 측면에서는 큰 이점을 볼 수 있을 것 같습니다.
여기까지 간단하게 데이터를 활용하여 모델을 학습하는 총과정을 밟아 보았습니다. 지금까지 배운 내용을 적용하는 느낌으로 작성하였고 여기에 더하여 GridSearchCV를 이용하여 모델의 최적의 파라미터를 찾는다거나, EDA 과정에서 데이터 전처리를 더 정교하게 하는 등의 여러 가지 방법으로 모델의 성능을 향상할 수 있을 것 같습니다!
출처
[데싸라면, 빨간색 물고기, 자투리코드] 파이썬 한권으로 끝내기: 데이터분석전문가(ADP) + 빅데이터분석기사 실기대비, 시대고시기획(2022)
'Data Science > Pandas' 카테고리의 다른 글
| pandas의 transform 함수 (apply 함수와의 차이) (0) | 2023.09.05 |
|---|---|
| Pandas로 datetime 다루기 (0) | 2023.09.04 |
| GridSearch를 이용한 model training (0) | 2023.09.01 |
| 결측치 처리 - KNNImputer (0) | 2023.09.01 |
| Confusion Matrix - 혼동행렬 (0) | 2023.09.01 |



