728x90
반응형
✔️ 오늘의 리트코드 공부 기록 – Unique Paths
문제 요약
m x n 격자가 주어지고, 오른쪽 또는 아래로만 이동할 때 가능한 경로의 수를 구하라.
- 문제 링크: https://leetcode.com/problems/unique-paths
🤔 처음 떠올린 아이디어
도착점까지 항상 아래, 오른쪽으로만 갈 수 있으므로,
행을 위에서부터 내려오면서 각 칸의 경로 수를 갱신하면 어떨까라는 생각이 들었다.
- 첫 행과 첫 열은 이동 방향이 하나뿐이므로 1로 초기화
- 나머지 칸은 위쪽과 왼쪽에서 오는 경로 수의 합으로 계산
💡 핵심 깨달음: DP로 점화식 세우기
각 칸 (r,c)까지 올 수 있는 경로 수 =
위에서 오는 경로 수 + 왼쪽에서 오는 경로 수
즉, dp[r][c] = dp[r-1][c] + dp[r][c-1]
코드 Java
1️⃣ 2차원 배열 DP (직관적 버전)
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 첫 행과 첫 열 초기화
for (int r = 0; r < m; r++) dp[r][0] = 1;
for (int c = 0; c < n; c++) dp[0][c] = 1;
// DP 점화식: dp[r][c] = 위 + 왼쪽
for (int r = 1; r < m; r++) {
for (int c = 1; c < n; c++) {
dp[r][c] = dp[r-1][c] + dp[r][c-1];
}
}
return dp[m-1][n-1];
}
}
직관적이고 이해하기 쉽지만, 공간 O(m*n)
2️⃣ 1차원 배열 DP (공간 최적화)
- 2차원 배열 DP에서, 현재 행 계산에는 바로 위 행과 왼쪽 칸 값만 필요
- 이전 행 전체를 저장할 필요가 없으므로 1차원 배열 하나만으로도 계산 가능
class Solution {
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
// 첫 행 초기화
for (int i = 0; i < n; i++) dp[i] = 1;
// DP 계산
for (int r = 1; r < m; r++) {
for (int c = 1; c < n; c++) {
dp[c] += dp[c-1];
}
}
return dp[n-1];
}
}
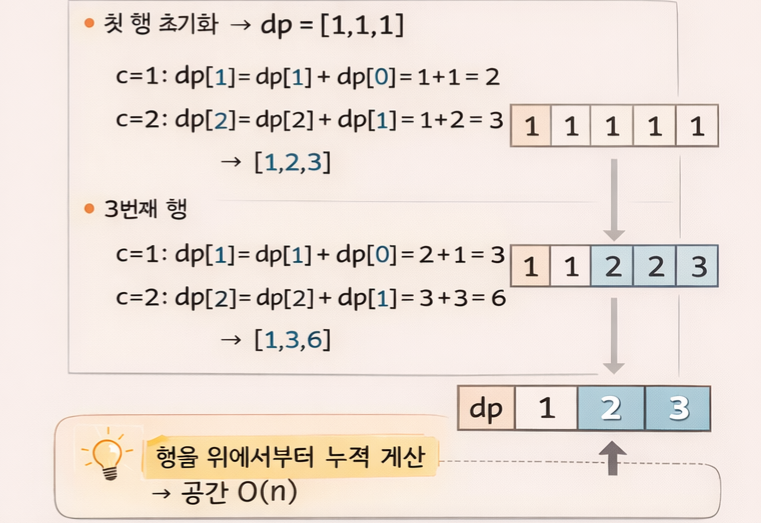
💡 핵심: 왼쪽값(dp[c-1])을 더하면서 갱신 → 이전 행(dp[c]) + 현재 왼쪽 칸(dp[c-1])
→ 한 행씩 위에서 아래로 누적하면서 계산 → 공간 O(n) 최적화
📈 시간/공간 복잡도
- 시간: 모든 칸을 한 번씩 계산 → O(m*n)
- 공간: 2D 배열 O(m*n) / 1D 배열 O(n)
📝 이번 문제에서 얻은 깨달음
- DP의 핵심: “각 위치까지 도달하는 방법을 미리 계산”
- 2D DP → 직관적, 이해 쉬움
- 1D DP → 공간 효율적, 코드 짧음
- 결국 중요한 건 단순히 공식을 외우는 것이 아니라, “경로 누적 개념”을 이해하는 것
728x90
반응형
'Algorithms' 카테고리의 다른 글
| [LeetCode] 76. Minimum Window Substring 풀이 (Java) (0) | 2026.01.26 |
|---|---|
| [LeetCode] 73. Set Matrix Zeroes 풀이 (Java) (0) | 2026.01.25 |
| [LeetCode] 56. Merge Intervals 풀이 (Java) (0) | 2026.01.21 |
| [LeetCode] 55. Jump Game 풀이 (Java) (1) | 2026.01.20 |
| [LeetCode] 54. Spiral Matrix 풀이 (Java) (0) | 2026.01.19 |
