이번 포스팅은 『가상 면접 사례로 배우는 대규모 시스템 설계 기초 1권』 6장을 공부하며 배웠던 개념들에 대하여 정리하였습니다.
해당 장에서는 데이터 관리를 여러 노드에 복제한 분산 시스템으로 설계하고 있는데요, 이때 자연스럽게 발생하는 문제들이 있습니다. 바로 데이터 불일치, 정합성 문제, 동기화 지연 등압나다.
『가상 면접 사례로 배우는 대규모 시스템 설계 기초 1권』의 6장은 이런 상황에서 어떤 기술들이 실제로 사용되는지를 설명해주고 있어 공부하면서 궁금했던 개념들을 정리해 보았습니다.
🧠 분산 시스템을 이해하기 위한 핵심 개념
— 머클 트리, Anti-entropy, 벡터 버저닝까지
우선 머클 트리와 Anti-entropy는 분산 환경에서 특정 노드에 장애가 발생했을 때 일관성이 깨진 데이터에 대하여 어떻게 장애 처리를 할 수 있을지에 대해서 설명합니다.
벡터 버저닝의 경우, 데이터를 다중화하였을 때 (즉, 동일한 데이터를 N 개 서버에 사본을 저장) 발생할 수 있는 사본 간 일관성이 깨지는 문제를 어떻게 해결할 수 있는지에 대해 설명합니다.
🌳 1. 머클 트리 (Merkle Tree)
👉 정의
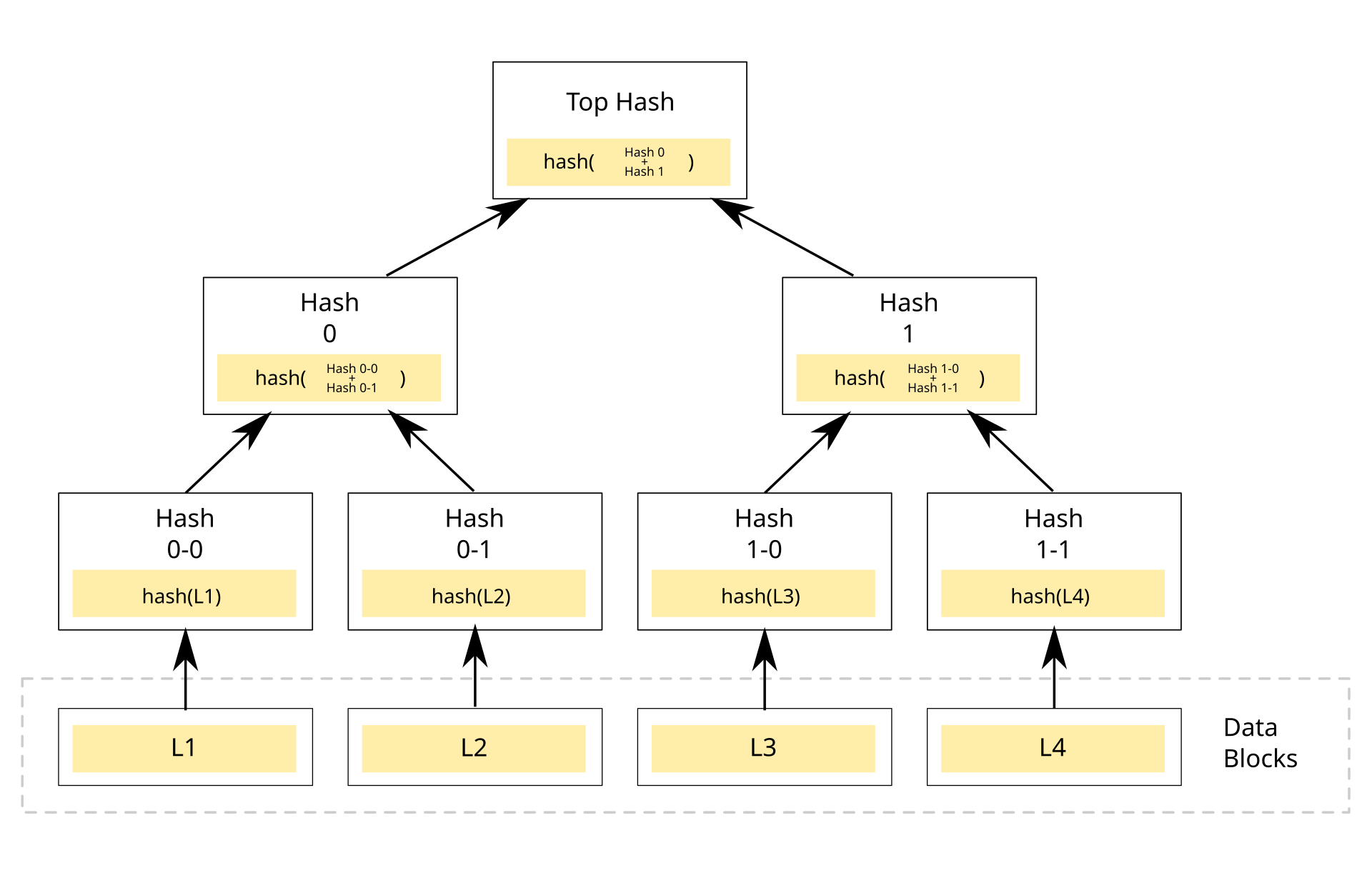
머클 트리는 데이터를 해시로 요약하고, 이 해시들을 트리 구조로 구성한 자료구조 입니다.
루트(root) 해시 하나만으로 전체 데이터의 무결성을 검증할 수 있고, 일부만 비교해서도 어떤 부분이 달라졌는지 빠르게 파악할 수 있습니다.
🧩 구조
(그림 출처: https://ko.wikipedia.org/wiki/해시_트리#/media/파일:Hash_Tree.svg)
- Leaf Node: 각 데이터 블록의 해시
- Internal Node: 자식 노드의 해시 두 개를 합쳐 다시 해시
- Root: 최상단 해시 하나로 전체 요약
🛠️ 사용처
- Git: 버전 관리 (파일 변경 추적)
- 블록체인: 트랜잭션(거래 내역) 무결성
- 분산 키-값 저장소 (Dynamo, Cassandra 등): 노드 간 데이터 비교 및 동기화
🍊 비유
바구니에 과일 8개가 있을 때, 각 과일에 해시 스티커를 붙이고, 그걸 계속 묶어 최종 스티커 하나만(루트 해시) 보여줘서 "이 바구니 안의 과일은 안 바뀌었어!"는 걸 증명하는 구조.
🔁 2. Anti-Entropy (무질서 제거 프로토콜)
👉 정의
"Entropy"가 물리학에서 ‘무질서’를 뜻하듯, Anti-entropy는 무질서를 정리하는 작업입니다.
즉, 분산 시스템에서는 장애, 지연 등으로 인해 노드 간의 데이터가 불일치할 수 밖에 없는데, 노드 간의 데이터 불일치를 감지하고 수정하는 동기화 해서 맞춰주는 역학을 합니다.
📌 특징
(그림 출처: https://umbum.dev/1300/)
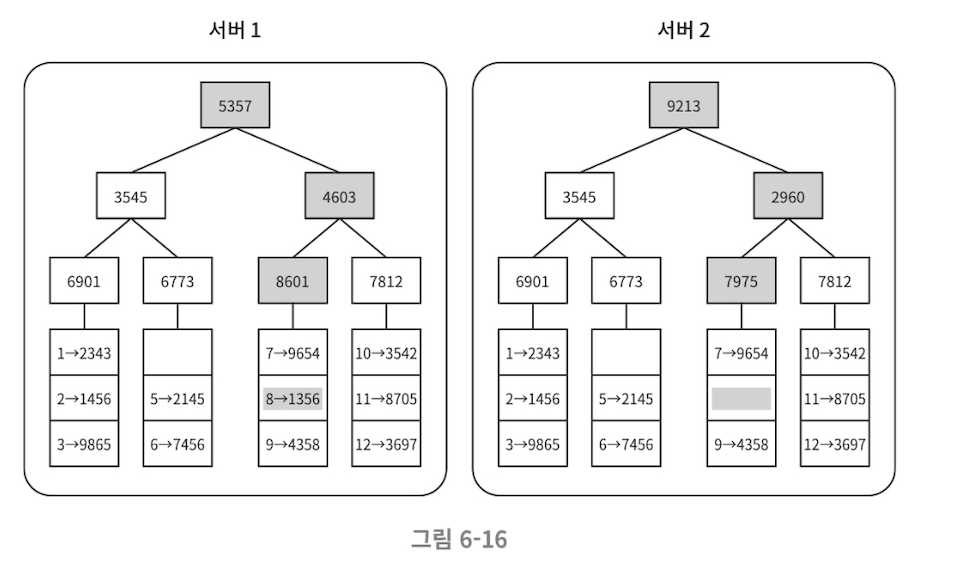
- 머클 트리를 사용하여 효율적으로 동기화합니다.
- 위 그림에서 루트부터 비교해서 루트가 다르므로 왼쪽과 오른쪽을 순서대로 비교합니다. 그리고 그 아래도 왼쪽 오른쪽을 반복적으로 비교하여 최종적으로 어디에서 데이터 불일치가 발생했는지 발견할 수 있습니다.
- 변경된 일부만 다시 복제합니다. (전체 복제 ❌)
🧠 예시
- NodeA와 NodeB가 각각 머클 트리를 만들고 루트 해시를 비교함
- 같으면 → 정합성 OK
- 다르면 → 서브트리를 비교하며 차이 나는 키만 복제
💡 왜 중요할까?
네트워크 지연, 장애 등으로 일부 노드 데이터가 어긋날 수밖에 없는 분산 환경에서 최소한의 비용으로 정합성을 유지하는 핵심 기술. 즉, 매번 전체 데이터를 Ctrl+C, Ctrl+V 하는 것이 아닌, 바뀐 부분만 Ctrl+C, Ctrl+V 하는 스마트한 방법.
🕰️ 3. 벡터 버저닝 (Vector Clock)
👉 정의
분산 환경에서는 서로 다른 노드에서 동시에 같은 데이터를 수정할 수 있습니다. 이 때, 누가 먼저 수정했는지 판단하기 위한 버전 관리 기법 으로 단순한 숫자 버전 대신, 각 노드별 수정 횟수를 기록한 “벡터” 형태로 버전을 표현한다.
📦 형태
{ "NodeA": 2, "NodeB": 1 }- 이 벡터는 “NodeA는 2번, NodeB는 1번 수정함”이라는 의미
- 이런 형태의 벡터들의 버전을 비교해서 누가 최신인지, 충돌인지 판단 가능
⚔️ 충돌 판단법
| 비교 결과 | 의미 | 충돌 여부 |
|---|---|---|
| 모든 항목에서 A ≥ B, 하나는 > | A가 B의 후손 | ❌ |
| 반대 | B가 A의 후손 | ❌ |
| 서로 어떤 노드는 A > B, 어떤 건 B > A | 서로 독립적으로 수정 | ✅ 충돌 |
🧠 예시
- A:
{NodeA: 2}, B:{NodeB: 1}→ 서로 독립적인 수정 → 충돌 발생 - A:
{NodeA: 1}, B:{NodeA: 2}→ B가 A의 후속 → 충돌 아님 - A:
{NodeA: 2, NodeB:1}, B:{NodeA: 1, NodeB: 2}→ 충돌 발생
🤹 충돌 해결
- 시스템은 충돌난 버전을 동시에 저장 (siblings)
- 이를 나중에 병합하거나, 애플리케이션 혹은 사용자가 선택
🧠 세 개념의 연결
| 상황 | 사용 기술 | 역할 |
|---|---|---|
| 전체 데이터가 같은지 빠르게 확인하고 싶을 때 | 머클 트리 | 트리 구조로 전체 요약, 빠른 비교 |
| 두 노드의 데이터가 일치하는지 주기적으로 점검할 때 | Anti-entropy | 머클 트리를 활용한 동기화 프로토콜 |
| 어떤 데이터 버전이 최신인지, 충돌인지 판단해야 할 때 | 벡터 버저닝 | 노드별 수정 이력 기반 비교 |
📌 마무리 요약
✅ 머클 트리는 데이터를 효율적으로 요약하고 비교하는 도구
✅ Anti-entropy는 노드 간 데이터 불일치를 탐지하고 고치는 과정
✅ 벡터 버저닝은 데이터 버전의 충돌 여부를 판단하고, 그 이력을 추적하는 방식
이 세 가지는 결국, 분산 환경에서도 신뢰할 수 있는 데이터 동기화와 정합성을 유지하기 위한 핵심 도구들입니다.
'Study' 카테고리의 다른 글
| 🚦 대규모 시스템 설계 기초 1권 – 4장: 처리율 제한 (Rate Limiting) (2) | 2025.06.20 |
|---|---|
| 대규모 시스템 설계 기초 2 - 6장. 광고 클릭 이벤트 집계 (0) | 2024.11.21 |
| 대규모 시스템 설계 기초 2 - 5장. 지표 모니터링 및 경보 시스템 (3) | 2024.11.16 |
| 대규모 시스템 설계 기초 2 - 4장. 분산 메시지 큐 (3) | 2024.11.07 |
| 대규모 시스템 설계 기초 2 - 3장. 구글맵 (0) | 2024.11.02 |


